Data Structures and Algorithm Programming
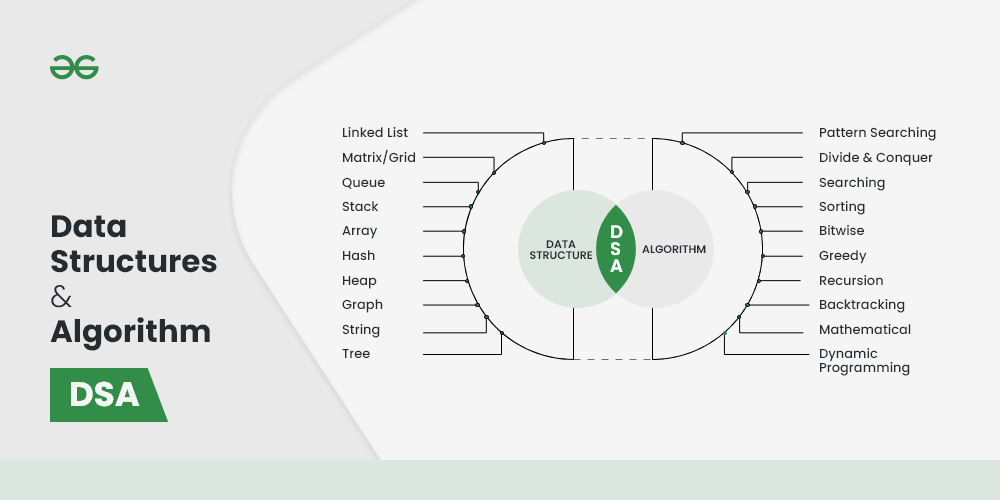
Data Structures and Algorithms (DSA) are fundamental concepts in computer science and software development. They are essential for efficiently storing, managing, and manipulating data, as well as solving complex problems using systematic approaches. A strong understanding of data structures and algorithms is crucial for writing efficient and scalable code. Data Structures: Data structures are organized ways to store, manage, and retrieve data. They define the relationship between the data, as well as the operations that can be performed on the data. Different data structures are suited to different kinds of applications, and knowing how to choose the right one for a particular task is a critical skill. Common Data Structures: Arrays: Description: An array is a collection of elements, each identified by an index or key. Elements are stored in contiguous memory locations, which allows for fast access to data. Use Cases: Arrays are used when you need fast access to data and the number of elements is known and fixed. They are common in situations like storing a list of items, implementing other data structures, and performing matrix operations. Linked Lists: Description: A linked list is a linear collection of elements, called nodes, where each node contains a data element and a reference (or link) to the next node in the sequence. Linked lists can be singly linked (one direction) or doubly linked (two directions). Use Cases: Linked lists are useful when the number of elements is unknown or dynamic, and you need efficient insertions and deletions, such as in implementing queues, stacks, or dynamic memory allocation. Stacks: Description: A stack is a linear data structure that follows the Last In, First Out (LIFO) principle. The most recent element added (pushed) to the stack is the first one to be removed (popped). Use Cases: Stacks are used in situations where you need to reverse a collection of items, backtrack in algorithms, or manage function calls in recursion. Queues: Description: A queue is a linear data structure that follows the First In, First Out (FIFO) principle. The first element added to the queue is the first one to be removed. Use Cases: Queues are used in scenarios that require ordering and processing elements sequentially, such as scheduling tasks, managing resources in shared systems, and implementing breadth-first search (BFS). Trees: Description: A tree is a hierarchical data structure consisting of nodes, with a single node designated as the root. Each node has zero or more child nodes, and the nodes with no children are called leaves. Common types of trees include binary trees, binary search trees (BST), AVL trees, and heaps. Use Cases: Trees are used in situations where hierarchical data representation is required, such as in file systems, databases (B-trees), expression evaluation, and organizing data for fast retrieval (binary search trees). Graphs: Description: A graph is a collection of nodes (vertices) connected by edges. Graphs can be directed or undirected and may or may not have weights associated with the edges. Use Cases: Graphs are used to model relationships between objects, such as social networks, web page linking (web graphs), network routing, and solving problems like shortest path (Dijkstra's algorithm), and network flow. Hash Tables: Description: A hash table is a data structure that maps keys to values using a hash function, which computes an index into an array of buckets or slots from which the desired value can be found. Use Cases: Hash tables are used for fast data retrieval, implementing associative arrays, caching, and situations where you need constant-time complexity for search, insert, and delete operations. Algorithms: Algorithms are step-by-step procedures or formulas for solving a problem or performing a task. They can be simple (like searching for an element in an array) or complex (like finding the shortest path in a graph). The efficiency of an algorithm is crucial in determining how well it performs with larger datasets. Key Algorithm Concepts: Time Complexity: Description: Time complexity is a measure of the amount of time an algorithm takes to complete as a function of the size of its input. It is often expressed using Big O notation, which classifies algorithms based on their growth rates, such as O(1), O(n), O(log n), O(n^2), etc. Use Cases: Time complexity helps in evaluating and comparing the efficiency of different algorithms, especially for large inputs. Space Complexity: Description: Space complexity refers to the amount of memory an algorithm needs to run to completion. Like time complexity, space complexity is also expressed in Big O notation. Use Cases: Space complexity is important when memory resources are limited or when working with large datasets. Sorting Algorithms: Description: Sorting algorithms arrange the elements of a list in a specific order (e.g., ascending or descending). Common sorting algorithms include: Bubble Sort: Simple, compares adjacent elements and swaps them if they are in the wrong order. (O(n^2)) Selection Sort: Repeatedly selects the minimum element and places it in the correct position. (O(n^2)) Insertion Sort: Builds the final sorted array one item at a time. (O(n^2)) Merge Sort: Divides the array into halves, sorts them, and merges them. (O(n log n)) Quick Sort: Picks a pivot and partitions the array around the pivot. (O(n log n) average) Use Cases: Sorting is a fundamental operation in computer science used in tasks like searching, data analysis, and optimizing algorithms. Searching Algorithms: Description: Searching algorithms are used to find specific elements within a data structure. Common searching algorithms include: Linear Search: Scans each element until it finds the target. (O(n)) Binary Search: Efficiently searches a sorted array by repeatedly dividing the search interval in half. (O(log n)) Use Cases: Searching is essential in databases, file systems, and applications where quick access to data is needed. Dynamic Programming: Description: Dynamic programming is a technique for solving complex problems by breaking them down into simpler subproblems and solving each subproblem only once, storing the results for future reference (memoization). It is particularly useful for optimization problems. Use Cases: Dynamic programming is used in problems like the knapsack problem, shortest path in a weighted graph, and sequence alignment in bioinformatics. Greedy Algorithms: Description: Greedy algorithms build up a solution piece by piece, always choosing the next piece that offers the most immediate benefit (the "greedy" choice). This approach does not always lead to the optimal solution but works well for certain problems. Use Cases: Greedy algorithms are used in tasks like finding the minimum spanning tree (Kruskal’s or Prim’s algorithm), Huffman coding, and coin change problems. Divide and Conquer: Description: Divide and conquer is an algorithmic paradigm that breaks a problem down into smaller subproblems, solves each subproblem recursively, and then combines their solutions to solve the original problem. Use Cases: This approach is used in algorithms like merge sort, quick sort, and fast Fourier transform (FFT). Backtracking: Description: Backtracking is a technique for solving problems by trying out different solutions and undoing ("backtracking") when a solution does not work. It is commonly used for solving constraint satisfaction problems. Use Cases: Backtracking is used in puzzles like the N-Queens problem, Sudoku solvers, and combinatorial optimization problems. Importance of Data Structures and Algorithms: Efficiency: Understanding DSA allows developers to write code that can handle large amounts of data efficiently. The choice of the right data structure and algorithm can significantly reduce the time and space required for a program. Problem Solving: DSA provides a foundation for solving complex computational problems. It teaches a systematic approach to breaking down problems, designing solutions, and optimizing performance. Scalability: Well-designed algorithms and data structures ensure that software can scale effectively as the amount of data or the number of users grows. Foundation for Advanced Topics: Knowledge of DSA is essential for understanding more advanced topics in computer science, such as machine learning, artificial intelligence, database management, and operating systems.